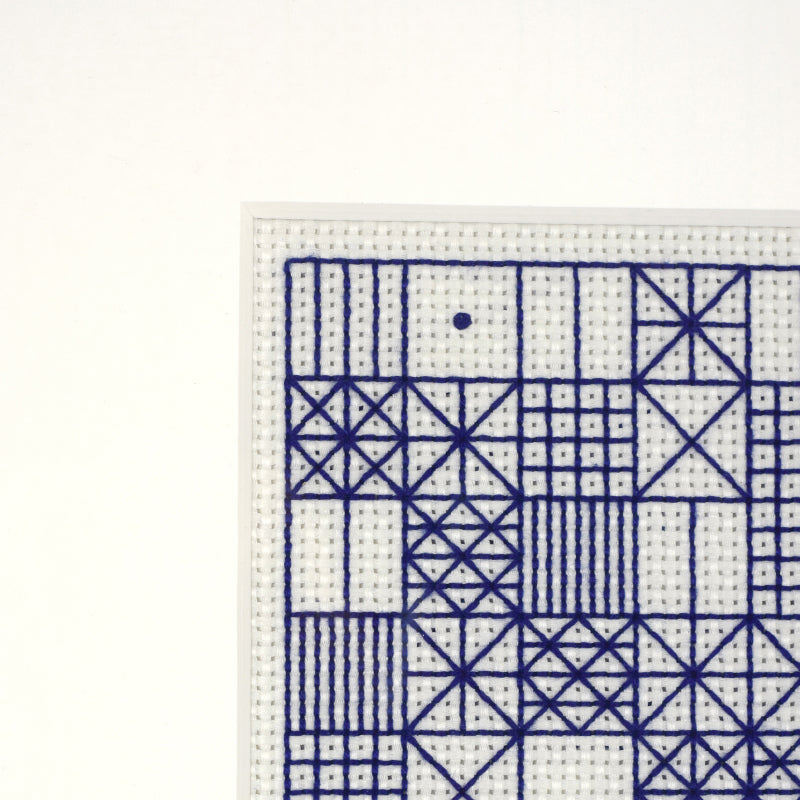
Embroidery and Fabric Design
We have used the concept of squaring the circle as inspiration for a new pattern. In order to express Pi in a visual way we created coded units that represent numbers 0-9 and used the number pi to generate the sequence.


There is an ancient greek mathematical problem created as an exercise for aspiring mathematicians to try and solve. It involves using a compass and a straight edge to create a square with an equal area as a given circle.
The problem involves using Pi to calculate the area of the circle, but as Pi is an irrational number the result can never be exactly the same area as the square.
Pi has infinite decimal points, that never settle into a permanent repeating pattern, and therefore it is impossible to solve the problem.


Circle and square with equal areas or approximate equal areas.
Squaring the circle by creating a circle and a square with equal areas:
Squaring the circle involves creating a circle with a circumference equal to the perimeter of a square. Also squaring the circle can involve creating a circle and a square with equal areas or approximate equal areas. Squaring the circle can also include harmonious relationships such as the part of the square that intersects the circle’s circumference can be similar to the radius of the circle or the same as the radius of the circle or equal to half of the square’s edge length. Squaring the circle with the area of the square being equal to the area of the circle usually cannot be achieved with 100% accuracy because traditional Pi 3.141592653589793 has been proven to be Transcendental in addition to being irrational. Traditional Pi 3.141592653589793 is Transcendental because Traditional Pi 3.141592653589793 does not fit any polynomial equations. Squaring the circle becomes possible and easy after traditional Pi 3.141592653589793 has been rejected and replaced with other values of Pi that are NOT transcendental. Golden Pi = 3.144605511029693 is irrational but Golden Pi is NOT transcendental because Golden Pi = 3.144605511029693 is the only value of Pi that fits the following polynomial equations: 8th degree polynomial for Golden Pi: π8 + 16π6 + 163π2 = 164.
4th dimensional equation/polynomial for Golden Pi = 3.144605511029693 (x4 + 16×2 – 256 = 0).
A polynomial is an expression consisting of variables (or indeterminates) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example in three variables is x3 + 2xyz2 − yz + 1.
Polynomials appear in a wide variety of areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated problems in the sciences; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, central concepts in algebra and algebraic geometry.
Both Golden Pi = 3.144605511029693 and Pi accepted as 22 divided by 7 = 3.142857142857143 can be used to create a circle and a square with equal areas of measure involving 100% accuracy.My question is it possible to create a circle with a surface area of 106 equal units because if we can create a circle with a surface area of 106 equal units of measure then we can also create a square with a surface area of 106 equal units of measure by creating a scalene triangle with the second longest edge length as 9 equal units of measure taken from the diameter of the circle that has a surface area of 106 equal units of measure, while the shortest length of the scalene triangle has 5 equal units of measure. The hypotenuse of a scalene triangle with the second longest length as 9 equal units of measure and the shortest length of the scalene triangle as 5 equal units of measure is equal in measure to the width of a square that has a surface area of 106 equal units of measure. We can use the theorem of Pythagoras: to prove that the square with a width equal to the longest length of the scalene right triangle also called the hypotenuse also has 106 equal units of measure.
Area of circle = 106.
Rational measure for the diameter of circle = 11.62.
Irrational measure for the diameter of the circle = 11.61180790611399 according to Golden Pi = 3.144605511029693.
Irrational measure for the diameter of the circle = 11.61180790611399 divided by the width of the square the square root of 106 = the square root of the Golden root = 1.127838485561683.
The Golden root = 1.272019649514069.The Golden root = 1.272019649514069 is the square root of Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
Irrational measure for the circumference of the circle = 36.514555134584213 according to Golden Pi = 3.144605511029693.
Square root of Golden Pi = 3.144605511029693 = 1.773303558624324
9 squared = 81.
5 squared = 25.
81 + 25 = 106.
Most values of Pi can confirm that if a circle has a rational measure for the diameter as 11.62 equal units of measure then the surface area of the circle with a rational measure for the diameter of 11.62 equal units of measure is 106 equal units of measure.
Is it possible to create a circle with a surface area of 154 equal units because if we can create a circle with a surface area of 154 equal units of measure then we can also create a square with a surface area of 154 equal units of measure by creating a scalene triangle with the second longest edge length as 12 equal units of measure taken from the diameter of the circle that has a surface area of 154 equal units of measure, while the shortest length of the scalene triangle has 4 equal units of measure. The hypotenuse of a scalene triangle with the second longest length as 12 equal units of measure and the shortest length of the scalene triangle as 4 equal units of measure is equal in measure to the width of a square that has a surface area of 154 equal units of measure. We can use the theorem of Pythagoras: to prove that the square with a width equal to the longest length of the scalene right triangle also called the hypotenuse also has a surface area of 154 equal units of measure.
Area of circle = 154.
Diameter of circle = 14.
Circumference of circle = 44.
Ancient Egyptian Pi = 22 divided by 7 = 3.142857142857143.
12 squared = 144.
3 squared = 9.
1 squared = 1
144 + 9 + 1 = 154.
“The ancient Egyptian square root of Pi rectangle and the ancient Egyptian square root for the Golden root rectangle and also the Pythagorean theorem”:
A square with a surface area of 154 equal units of measure can be created if the second longest edge length of a scalene right triangle has 12 equal units of measure while the shortest edge length of the scalene right triangle has 4 equal units of measure. According to the Pythagorean theorem if a square has a width that is equal to the hypotenuse of a scalene right triangle that has its second longest edge length as 12 equal units of measure while the shortest edge length for the scalene right triangle has 4 equal units of measure then the surface area of the square that has a width equal to the measure of the hypotenuse for the scalene right triangle that has its second longest edge length as 12 while its shortest edge length is 4 is 154 equal units of measure. If the width of the square that has a surface area of 154 equal units of measure is then accepted as the longer length of a square root of ancient Egyptian Pi = 1.772810520855837 rectangle then a circle can be created with the shorter edge length of the square root of ancient Egyptian Pi = 1.772810520855837 rectangle being equal in measure to the radius of the circle with a surface area equal to the surface area of the square that has a surface are of 154 equal units of measure. According to ancient Egyptian Pi = 3.142857142857143 if the radius of a circle has 7 equal units of measure then the surface are of the circle is 154 equal units of measure. The measuring angles for a square root of ancient Egyptian Pi = 1.772810520855837 rectangle are 60.57369496075449 degrees and 29.42630503924551 degrees. 60.57369496075449 degrees can be gained when the square root of ancient Egyptian Pi = 1.772810520855837 is applied to the inverse of Tangent in Trigonometry. 29.4263050392455 degrees can be gained when the ratio 0.564076074817766 is applied to the inverse of Tangent in Trigonometry. If a circle with a diameter of 14 equal units of measure has already been created so that the surface area of the circle can have 154 equal units of measure according to ancient Egyptian Pi = 3.142857142857143 and the desire is to have a square that also has a surface area equal to the circle’s surface area of 154 equal units of measure then a solution is to add 1 quarter of the circle’s circumference hat is 11 to the diameter of the circle with 14 equal units of measure and at the division point where 14 is subtracted from the diameter line of 25 equal units of measure draw right angles that can touch the circumference of a circle or a semi-circle if the diameter of 25 equal units of measure is divided into 2 halves. A rectangle with its longest length as 14 while its second longest length is the square root of 154 has the ratio for the square root of the Golden root as 1.128152149635533. 1.128152149635533 is the square root of 1.272727272727273. 4 divided by 1.272727272727273 is ancient Egyptian Pi = 3.142857142857143. So the longer length of the ancient Egyptian square root for the Golden root = 1.128152149635533 rectangle is 14, the diameter of the circle with a surface area of 154, while the shorter length of the ancient Egyptian square root for the Golden root = 1.128152149635533 rectangle is the square root of 154 = 12.40967364599086, the width of the square.
1.128152149635532 squared is 1.272727272727272 and 1.272727272727272 squared is the Golden ratio of 1.619834710743799.
The ancient Egyptian square root for the Golden root = 1.128152149635532 is important.
i think its a miracle creating design in a mathmatical